Maxwell's Equations
This article was initially written as part of the IEEE STARS program.
Citation
Maxwell’s Equations provide a complete description of electromagnetic phenomena and underpin all modern information and communication technologies. They are named after James Clerk Maxwell, the Scottish physicist whose pioneering work during the second half of the 19th century unified the theories of electricity, magnetism, and light. The theory of electromagnetism was built on the discoveries and advances of many scientists and engineers, but the pivotal contribution was that of Maxwell. Today, Maxwell’s Equations are the essential tools of electrical engineers in the design all types of electrical and electronic equipment.
Introduction
Maxwell’s Equations provide a complete description of electromagnetic phenomena and underpin all modern information and communication technologies. They are named after James Clerk Maxwell (Figure 1), the Scottish physicist whose pioneering work unified the theories of electricity, magnetism, and light. Today, Maxwell’s Equations are the essential tool of electrical engineers, used to design all electrical and electronic equipment from cell phones to satellites, televisions to computers and power stations to washing machines. The theory of electromagnetism was built on the discoveries and advances of many scientists and engineers, but the pivotal contribution was that of Maxwell, who during the second half of the 19th century made the huge conceptual leaps that would enable the great advances in electrical technology throughout the 20th century.
The four equations
To set the context for the discovery and development of Maxwell’s Equations it is first important to understand what they are. In the modern context, Maxwell’s Equations refer to a set of four relations that describe the properties and interrelations of electric and magnetic fields. The equations are shown in modern notation in Figure 2. The electric force fields are described by the quantities E (the electric field) and D = εE (the electric displacement), the latter including how the electrical charges in a material become polarized in an electric field. The magnetic force fields are described by H (the magnetic field) and B = µH (the magnetic flux density), the latter accounting for the magnetization of a material.
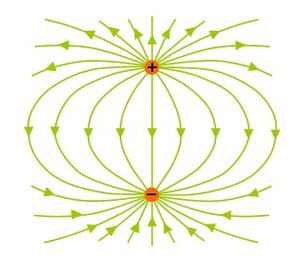
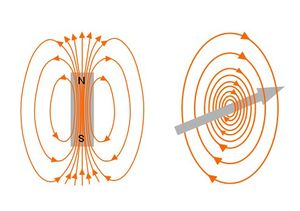
The equations can be considered in two pairs. The first pair consists of Equation 1 and Equation 2. Equation 1 describes the electric force field surrounding a distribution of electric charge ρ. It shows that the electric field lines diverge from areas of positive charge and converge onto areas of negative charge (Figure 3). Equation 2 shows that magnetic field lines curl to form closed loops (Figure 4), with the implication that every north pole of a magnet is accompanied by a south pole. The second pair, Equation 3 and Equation 4, describes how electric and magnetic fields are related. Equation 3 describes how a time-varying magnetic field will cause an electric field to curl around it. Equation 4 describes how a magnetic field curls around a time-varying electric field or an electric current flowing in a conductor.
These equations can explain how your hair stands on end when you remove your nylon sweater, how a compass needle always points north, how a power station turbine can generate electricity, and how a loudspeaker can convert an electric current into sound. When combined these equations also describe the transmission of radio waves and the propagation of light.
The emergence of electromagnetism
The sciences of electricity and magnetism and their fusion as electromagnetism evolved through a series of advances from many different scientists. To name all involved would amount to writing a Who’s Who of 18th and 19th century physics. Here we will concentrate on the contributions most directly related to the development of Maxwell’s Equations. The advances through the 18th century in understanding electric charges and currents, notably the work of Benjamin Franklin and Alessandro Volta culminated in the work of Charles Coulomb, whose law showed that the strength of electric force varied inversely with the square of the distance to a positively or negatively charged object. This law, and a similar one for magnets, was later generalized by the work of Poisson and Gauss in the early 19th century leading to Gauss’ Law, the physics behind the first of Maxwell’s Equations.
Up to this time, the laws of electricity and the laws of magnetism were regarded as two separate fields of physics. This changed in September 1820 while Hans Christian Ørsted was setting up a demonstration for a lecture in Copenhagen: he discovered that an electric current can deflect the magnetic needle of a compass. News of Ørsted’s discovery spread quickly across Europe, and within a week Andre Ampère had shown the French Academy of Science in Paris that parallel currents in two wires attract each other, while opposite currents would repel. Soon after, Jean-Baptiste Biot and Philippe Savart showed the same forum how the strength of the force falls away with distance to the wire. Ampère’s relentless scientific efforts over the next six years founded the field of electrodynamics, with at times fortnightly reports to the French Academy of Sciences and the publication of his general law connecting electric currents with magnetic forces. Ampère’s work elegantly combined experiments and theory. Maxwell later described this as “one of the most beautiful achievements in science . . . from the brain of the Newton of electricity.”
Electromagnetism became a focus for the most eminent scientists of the 19th century. Of these the work of three men, Ampere, William Thomson, and Michael Faraday, would most directly influence Maxwell. Thomson, who later became Lord Kelvin, was a good friend of Maxwell’s, and the two regularly corresponded to discuss their scientific theories. The experiments of Michael Faraday, however, would have the greatest direct impact. Faraday was a self-educated scientist and exceptionally skilled experimentalist. During the 1820s and 1830s he made several key discoveries. He showed that a changing current in one circuit would induce a current in a neighboring circuit through a change in magnetic flux around the wires. He established how materials respond to electric fields, and this work led to the concepts of dielectric constant and polarization. (Thomson later devised the corresponding concepts for magnetism.) Through hundreds of experiments, Faraday showed that these effects could all be explained pictorially, using lines of force that fill the space around charges and currents. This was a new paradigm in physics - the force field - that would most strongly influence Maxwell.
Maxwell's theories
By the mid 19th century the various laws of electricity and magnetism were becoming well understood, and a common theory that could describe all phenomena was sought. Faraday’s vision of lines of force pervading space was radical, and the prevailing opinion of his contemporaries was that a theory should instead be based on forces acting at a distance, directly from one particle to another. On this basis Wilhelm Weber developed a theory linking Ampère’s and Faraday’s laws. However his theory was flawed as it required a condition that broke the law of energy conservation. Maxwell believed that Faraday was correct and in the 1850s, as a Fellow at the University of Cambridge, set about deriving a mathematical description of Faraday’s theory. In the paper "On Faraday’s Lines of Force," Maxwell used a fluid analogy to derive his first theory of electromagnetic force fields. The fluid analogy was limited in that it could describe only fields around static charges and steady electric currents. Maxwell also formulated mathematics for Faraday’s concepts of induced currents, but could not interpret these within the fluid model.
After a period focused on other topics, including color perception and the dynamics of Saturn’s rings, Maxwell returned to the problem of electromagnetism with a completely new theory. Now Professor of Natural Philosophy at King’s College London, Maxwell published the new theory in four parts between 1861 and 1862 in his landmark work “On Physical Lines of Force.” Here Maxwell devised a mechanical model that could account for all the known electromagnetic phenomena. His mechanical construct featured spinning cells and idle wheels that mimic the curling magnetic fields around currents in conductors. This gave a successful though somewhat improbable analogy that could describe Ampère’s, Faraday’s, and Gauss’ laws. Indeed Maxwell was careful to convey at the end of part II of “On Physical Lines of Force” that this model was an analogy and not a suggestion of the real mechanism.
At this stage the theory was successful but as yet incomplete, for it did not properly describe current flow through electrical capacitors. Maxwell contemplated this problem during the summer of 1861 while “in the country” at his family estate Glenlair in southwest Scotland. There he realized that if he made his mechanical construct elastic it would allow changing electric currents to propagate through non-conductors as they do in capacitors, and thereby corrected Ampère’s Law with a new term called the electric displacement current. This correction completed the essential physics of the theory and was published in the final two parts of “On Physical Lines of Force” in 1862. However, his original equations were in a quite different mathematical form from those used today.
Maxwell’s correction to his model had a dramatic implication. He realized that if the electromagnetic medium was elastic, then it would support oscillating waves. While at Glenlair he calculated a formula for the speed of these waves, and on his return to King’s College London in the fall of 1861 he found that this speed very closely matched the speed of light as measured by Hippolyte Fizeau. Maxwell commented “The velocity of transverse undulations in our hypothetical medium, calculated from the electro-magnetic experiments of MM. [Friedrich] Kohlrausch and [Wilhelm] Weber, agrees so exactly with the velocity of light calculated from the optical experiments of M. Fizeau, that we can scarcely avoid the inference that light consists in the transverse undulations of the same medium which is the cause of electric and magnetic phenomena.”

The contrived mechanical analogy and radical idea of force fields meant that others were slow to accept Maxwell’s theory. Three years later Maxwell published his third theory of electromagnetism. This was based only on the laws of dynamics, and so stripped away the mechanical scaffolding supporting his earlier model. In "A Dynamical Theory of the Electromagnetic Field," Maxwell collected together his equations of the electromagnetic field (Figure 5) and explicitly wrote down the electromagnetic wave equation. This paper was another landmark of physics in that it presented a theory that described all the known phenomena, but was independent of any underlying mechanical mechanism. This ultimately changed the way that physicists approached the development of new physical laws.
Maxwell subsequently left King’s College London and over the next six years worked as an independent scholar at Glenlair. During this time he wrote his magnum opus A Treatise on Electricity and Magnetism, published in 1873. In the Treatise he summarized the current state of knowledge of electromagnetism, presenting and developing his work alongside the theories of others. He further developed the mathematics, interpretation, and applications of his equations, and rewrote them in a more compact mathematical notation known as quaternions.
Subsequent developments
Over the next two decades Maxwell’s theory was accepted and advanced by others, notably Oliver Heaviside, Heinrich Hertz, and Hendrik Lorentz. Heaviside championed the Faraday-Maxwell approach to electromagnetism and simplified Maxwell’s original set of 20 equations to the four used today. Importantly, Heaviside rewrote Maxwell’s Equations in a form that involved only electric and magnetic fields. Maxwell’s original equations had included both fields and potentials. In an analogy to gravity, the field corresponds to the gravitational force pulling an object onto the Earth, while the potential corresponds to the shape of the landscape on which it stands. By configuring the equations only in terms of fields, Heaviside simplified them to his so-called Duplex notation, with the symmetry evident in the equations of Figure 2. He also developed the mathematical discipline of vector calculus with which to apply the equations. Heaviside analysed the interaction of electromagnetic waves with conductors and derived the telegrapher’s equations of Kirchhoff from Maxwell’s theory to describe the propagation of electrical signals along a transmission line.
Independently of Heaviside, Heinrich Hertz also derived a simplified version of Maxwell’s Equations, although he later acknowledged the precedence of Heaviside’s work. In 1888 Hertz made his most significant contribution with the discovery of radio waves. This confirmed Maxwell’s prediction of electromagnetic waves and thus validated the theory. Other notable contributions to electromagnetic wave theory include the work of Lorentz, Ludwig Boltzmann, and Hermann Helmholtz who developed Maxwell’s Equations to describe the propagation of light including reflection and refraction at surfaces.
Entering the 20th century, Maxwell’s Equations had impact beyond electromagnetism in the discovery of the theory of relativity and, decades later, the field equations of quantum mechanics. The work of both Hendrik Lorentz and Albert Einstein in deriving the theory of relativity was directly founded on the constant speed of light from Maxwell’s Equations. Einstein regarded Maxwell’s work as “the most profound and the most fruitful that physics has experienced since the time of Newton.” Quantum mechanics, though less clearly linked to electromagnetism, was nonetheless founded on the Faraday-Maxwell paradigm of the field theory. It should be noted that Maxwell based his theory on the concept of an aether, that is, an invisible all-penetrating medium through which the electromagnetic fields propagate. While it was established in 1892 after Maxwell’s death that no aether exists, the equations remain valid in their description of all electromagnetic phenomena.
The equations of electromagnetism have previously been known as the Hertz-Heaviside and Maxwell-Hertz Equations, but the term 'Maxwell’s Equations' was popularized by Einstein in 1940, in his monograph Considerations Concerning the Fundamentals of Theoretical Physics. In the modern context, Maxwell’s Equations are used in the design of all types of electrical and electronic equipment. The equations can only be solved exactly for simple structures of high symmetry. However the dramatic increase in computing power and development of numerical finite-difference techniques since the mid 1960s have enabled their widespread everyday use.
Timeline
- 1785, Coulomb’s Law is published
- 1812, Poisson’s Law is published
- 1813, Gauss’ Divergence Theorem is discovered
- 1820, H.C. Ørsted discovers that an electric current creates a magnetic field
- 1820, André-Marie Ampère’s work founds electrodynamics; Biot-Savart Law is discovered
- 1826, Ampère’s Law is published
- 1831, Faraday’s Law is published
- 1856, James Clerk Maxwell publishes "On Faraday’s lines of force"
- 1861, Maxwell publishes "On physical lines of force"
- 1865, Maxwell publishes "A dynamical theory of the electromagnetic field"
- 1873, Maxwell publishes Treatise on Electricity and Magnetism
- 1888, Heinrich Hertz discovers radio waves
- 1940, Albert Einstein popularizes the name 'Maxwell’s Equations'
- 1966, Kane Yee introduces finite-difference time domain methods to solve Maxwell’s Equations
Bibliography
References of Historical Significance
James Clerk Maxwell. 1856. “On Faraday’s lines of force”. Transactions of the Cambridge Philosophical Society, vol. 10 (1856), pp. 27-83
James Clerk Maxwell. 1862. “On physical lines of force”. Philosophical Magazine Series 4, vol. 21 (1861), pp. 161-175, 281-291, 338-348; Philosophical Magazine Series 4, vol. 23 (1862), pp. 12-24, 85-95
James Clerk Maxwell. 1865. “A dynamical theory of the electromagnetic field”. Philosophical Transactions of the Royal Society, vol. 155 (1865), p. 459-512
James Clerk Maxwell. 1873. A Treatise on Electromagnetism. Oxford: Clarendon Press, 1873
Oliver Heaviside. 1894. Electrical Papers. New York and London: Macmillan & Co, 1894
References for Further Reading
Martin Goldman. 1983. The Demon in the Aether: The Story of James Clerk Maxwell. Edinburgh: Paul Harris publishing, 1983
Basil Mahon. 2004. The Man who Changed Everything: The Life of James Clerk Maxwell. Chichester: Wiley, 2004
Paul J. Nahin. 1988. Oliver Heaviside: The Life, Work and Times of a Genius of the Victorian Age. New York: IEEE Press, 1988
P. Harman, editor. 2002. The Scientific Letters and Papers of James Clerk Maxwell. Cambridge: Cambridge University Press, 2002
Bruce J. Hunt. 1991. The Maxwellians. Ithaca, NY: Cornell University Press,1991
About the Author
Graham Turnbull is a senior lecturer in physics at the University of St Andrews in Scotland. He graduated with a first-class M.Sci. degree in physics and a Ph.D. in photonics, both from the University of St Andrews. After postdoctoral work at the University of Durham, he returned to St Andrews as faculty member of the School of Physics and Astronomy. Dr. Turnbull is a Senior Member of the IEEE and has served on the Scottish Chapter committee of the IEEE Photonics Society since 2003. In 2009 he led the installation of an IEEE Milestone to Maxwell’s Equations.