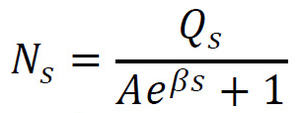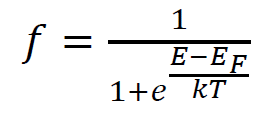On the origin of Fermi-Dirac statistics

From ETHW

This article in its original form was written by Giuseppe Pelosi and Massimiliano Pieraccini (University of Florence) in 2014.

Figure 1: Cover of the Italian scientific journal where Fermi published his preliminary work on quantum statistics in early 1924.
Figure 2: Ideal system of three electrons at the vertexes of an equilateral triangle.

The Italian-American Nobel laureate Enrico Fermi (Rome, Italy, 1901 – Chicago, Illinois, USA, 1954) is universally known for the so-called “Fermi-Dirac statistics” [1] that are the basis of the theory of conduction in metal and semiconductors, but not everybody knows how, when and where he conceived this fundamental contribution to modern electronics. Indeed, as we will show in this contribution, his mind was addressed to the theoretical issues that would lead him to "his" statistics since he was a young graduate, in Florence, Italy.

Significantly his graduation thesis for the Scuola Normale Superiore (a public learning institution in Pisa renowned for its excellence) on 22 June 1922 was entitled "Un teorema di calcolo delle probabilità ed alcune sue applicazioni” (A theorem on probability calculus and some of its applications) [2]. A year later he demonstrated another theorem about the ergodicity of the normal systems [3], but the key step torward the statistics named after him can be found in a paper he published in December 1924, in the Italian journal Il Nuovo Cimento [4] (See Figure 1).

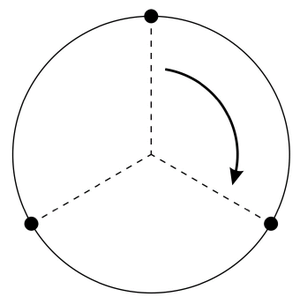
Fermi discusses the Wilson-Sommerfeld quantization rules [5], [6] for the case of a set of identical systems. He makes a simple and enlightening example. Let consider three electrons that can be disposed on a ring at the vertices of an equilateral triangle. If the electrons are distinguishable, only a 360° rotation could bring the system to the initial condition; but if the electrons are undistinguishable, any 120° rotation return the system to the initial condition (See Figure 2). Fermi notes the application of quantization rules gives different results for these two cases.

Therefore, since 1924 Fermi had known how to quantize a set of particles or atoms, but not how to dispose them in the energy levels. The missing piece of the puzzle was what today we call the “Pauli Exclusion Principle.” Many years after, when Fermi was in America, he regretted with his friend Emilio Segrè that if he had had a few more months he could have gotten it [7]. The point is, when he was aware of it? The article by Wolfang Pauli that introduced the Exclusion Principle was published in April 1925 [8], but at that time Fermi was engaged in experimental work in spectroscopy [9], so probably he did not read it. In July he was a member of the commission of the “state exam,” the final examination for high school students, a major commitment that surely distracted him from his research, as he complained in his letters [10]. In August he went on vacation to the Dolomite mountains with several friends, including the German physicist Ralph de Laer Kronig. Kronig wrote regularly to Pauli about his recent publication and was probably the contact point between Pauli and Fermi. .

On the other hand, the first public presentation of the statistical calculus by Fermi was on February, 7 1926 [11] at the Accademia dei Lincei (the Italian Scientific Academy); therefore the gestation of the idea can be located between summer 1925 and the end of the year. In this span of time Fermi taught “Mathematical Physics” and “Mechanics” [12] at the University of Florence to a “number infinitely small of students” as he wrote in a personal letter [13].

He published his major result before in the proceedings of Accademia dei Lincei [14] and after in the German journal Zeitschrift fur Physik [15] with more details. The key formula he derived is:

Eq1 FermiStatisticalFormula-Original.png

with Qs the degeneration of quantum state s, Ns the number of atoms in state s, and A and β constants.

This expression is a bit different from what we are accustomed to using:

Eq2 FermiDiracStatisticalFormula.png


with f probability of occupation of a state at energy E, Ef constant (the so-called Fermi energy), k Boltzman’s constant, T temperature.

In effect the two articles by Fermi did not have the resonance they deserved; the community of quantum scientists understood their value only after Dirac obtained it independently from the symmetry properties of the state function that describes a set of particles [16]. So, the expression of Fermi distribution we currently use is in effect the Dirac formulation.

References

  1. ↑ C. Bernardini and L. Bonolis, Enrico Fermi: his Work and Legacy, Springer, 2001.
  2. ↑ Enrico Fermi, Note e Memorie (Collected Papers), Accademia Nazionale dei Lincei and The University of Chicago Press, 2 Volumes, Roma and Chicago, 1961-1965.
  3. ↑ E. Fermi, “Dimostrazione che in generale un sistema meccanico normale è quasi ergodico,” Nuovo Cimento Vol. 25 (1923), p. 267-9.
  4. ↑ E. Fermi, “Considerazioni sulla quantizzazione dei sistemi che contengono degli elementi identici,” Il Nuovo Cimento 1, no. 1 (1924), p. 145-52.
  5. ↑ W. Wilson, “The Quantum Theory of Radiation and Line Spectra,” Philosophical Magazine 29 (1915), p. 795–802.
  6. ↑ A. Sommerfeld, "Zur Quantentheorie der Spektrallinien," Annalen der Physik, 356, no. 17 (1916), p. 1–94.
  7. ↑ E. Segre, Enrico Fermi Physicist, University of Chicago Press, 1970.
  8. ↑ W. Pauli, “Uber den Zusammenhang des Abschlusses der Elektronengruppen im Atom mit der Komplexstruktur der Spektren,” Zeitschrift fur Physik 31 (1925), p. 765-83.
  9. ↑ Enrico Fermi, Note e Memorie (Collected Papers), Accademia Nazionale dei Lincei and The University of Chicago Press, 2 Volumes, Roma and Chicago, 1961-1965.
  10. ↑ E. Segre, Enrico Fermi Physicist, University of Chicago Press, 1970.
  11. ↑ E. Fermi, “Sulla quantizzazione del gas perfetto monoatomico,” Atti dell’Accademia dei Lincei 3 (1926), p. 145-9.
  12. ↑ G. Pelosi, M. Pieraccini, and S. Selleri, “Enrico Fermi in Florence,” IEEE Antennas and Propagation Magazine 55, No. 6 (December 2013), p. 272-6.
  13. ↑ E. Segre, Enrico Fermi Physicist, University of Chicago Press, 1970.
  14. ↑ E. Fermi, “Sulla quantizzazione del gas perfetto monoatomico,” Atti dell’Accademia dei Lincei 3 (1926), p. 145-9.
  15. ↑ E. Fermi, “Zur Quantelung des idealen einatomigen Gases,” Zeitschrift für Physik 36 (1926), no. 11-12, p. 902-12.
  16. ↑ P.A.M. Dirac, “On the Theory of Quantum Mechanics,” Proceedings of the Royal Society (London) A112 (1926), pp. 281-305.
Retrieved from "https://ethw.org/w/index.php?title=On_the_origin_of_Fermi-Dirac_statistics&oldid=106396"

Powered by MediaWiki
Powered by Semantic MediaWiki